Funciones lineales y cuadráticas

Las funciones lineales y cuadráticas se pueden escribir de la forma f(x) = mx + b, y f(x) = ax2 + bx + c respectivamente, quieres saber a detalle que son las funciones lineales y cuadráticas, cómo se representan en la gráfica y algunos ejemplos? Sigue leyendo!

Funciones lineales

Una función lineal es una función polinómica de primer grado, en un gráfica se representa como una línea recta y se escribe: f(x) = mx + b.

Recordemos que los polinomios de primer grado tienen la variable elevada a la primera potencia, cuando la potencia es 1 normalmente no se escribe.

m = pendiente de la recta (constante).

b = punto de corte de la recta con el eje y (constante).

x = variable.

Cuando modificamos “m” en una función lineal se modifica la pendiente es decir la inclinación de la recta, si cambiamos “b” la línea se mueve hacía arriba o abajo.

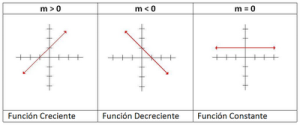
Las funciones se pueden clasificar en tres tipos:

Si el valor de “m” es mayor a cero la función es creciente.
Si el valor de “m” es menor a cero la función es decreciente.
Si “m” es igual a cero la función es constante (su gráfica será una recta paralela al eje X).

Estos son los tres tipos de funciones:

Haz click en la imagen para verla más grande

Ejemplo

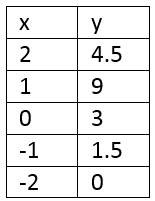
Tenemos la siguiente función: y = 1.5 x + 3

la pendiente es 3/2, cuando aumentamos x en una unidad “y” aumenta en 3/2 de unidad, b = 3 entonces la recta corta el eje y en el punto y = 3.

Para graficar podemos hacer una tabla de valores y graficamos cada punto en el plano cartesiano.

Funciones cuadráticas

Una función cuadrática es una función polinómica de segundo grado que se escribe : f(x) = ax2 + bx + c

a, b y c = números reales diferentes a cero.

Si a>0 el vértice de la parábola estará en la parte inferior y si o a<0 el vértice estará en la parte superior de la parábola.

La gráfica de una función cuadrática es una parábola de la cual el eje de simetría es paralelo al eye de las “y”.

Modificaciones en la función, si sumamos o restamos dentro del paréntesis la parábola se mueve hacia la izquierda o la derecha respectivamente, Si restamos o sumamos en la función fuera del paréntesis la parábola se mueve hacia abajo o hacia arriba.

Para obtener la raíces de la ecuación seguimos estos pasos:

Igualar la ecuación a cero.
Factorizar la ecuación.
Igualar cada factor a cero y obtener las raíces.

Para graficar la función seguimos estos pasos:

Con el valor de “a” determinar si la parábola abre hacía arriba o hacía abajo.
Obtener los puntos de intersección, los del eje “x” se obtienen con las raíces de la ecuación, para obtener las intersecciones en “y” igualamos la x a cero.
Obtener el vértice de la función, el punto “x” de la coordenada del vértice se obtiene con la fórmula -b/2a y el punto “y” se obtiene sustituyendo x en la función.
Graficar los puntos obtenidos en los puntos 2 y 3 para graficar la curva.
Raíces

Véase también: Ecuación de segundo grado

Las raíces (o ceros) de una función cuadrática, como en toda función, son los valores de x, para los cuales $a x^2 + bx + c = 0 \$ . Son denotadas habitualmente como: $x_1$ y $x_2$ , dependiendo del valor del discriminante Δ definido como $\Delta = b^2 - 4 a c \$ .
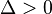- Dos soluciones reales y diferentes si el discriminante es positivo, $\Delta > 0$ :
$x_1 = \frac{-b + \sqrt {\Delta}}{2a}$

$x_2 = \frac{-b - \sqrt {\Delta}}{2a}$
- Corta la parábola al eje X en dos puntos diferentes.
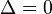- Una solución real(o solución doble) si el discriminante es cero, $\Delta = 0$ :
$x_1 = x_2 = -\frac{b}{2a}$
- La parábola es tangente al eje X.
- La parábola no corta al eje X.
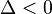- El único caso restante es que el discriminante sea negativo, $\Delta < 0$ .
En tal caso, las raíces no son reales, sino que son dos números complejos conjugados:

$x_1 = \frac{-b}{2a} + i \frac{\sqrt {-\Delta}}{2a}$

$x_2 = \frac{-b}{2a} - i \frac{\sqrt {-\Delta}}{2a}$

Representación analítica

Hay tres formas de escribir una función cuadrática, aplicables según el uso que se le quiera dar a la función, un estudio analítico de la función o de la ecuación cuadrática, una interpretación o construcción geométrica de la parábola, etc.

Forma desarrollada o polinómica

La forma desarrollada de una función cuadrática (o forma estándar) corresponde a la del polinomio de segundo grado, escrito convencionalmente como:

$f(x) = ax^2 + bx + c \,$

con $a \neq 0$ .

Forma factorizada

Toda función cuadrática se puede escribir en forma factorizada en función de sus raíces como:

$f(x) = a(x - x_1)(x - x_2) \,$

siendo a el coeficiente principal de la función, y $x_1$ y $x_2$ las raíces de $f(x)$ . En el caso de que el discriminante Δ sea igual a 0 entonces $x_1 = x_2$ por lo que la factorización adquiere la forma:

$f(x) = a(x - x_1)^2 \,$

En este caso a $x_1$ se la denomina raíz doble, ya que su orden de multiplicidad es 2. Si el discriminante es negativo, las soluciones son complejas, no cabe la factorización.³

Forma canónica

Toda función cuadrática puede ser expresada mediante el cuadrado de un binomio de la siguiente manera:

$f(x) = a (x - h)^2 + k \,$

siendo a el coeficiente principal y el par ordenado (h;k) las coordenadas del vértice de la parábola.

Representación gráfica

Intersección con el eje

La función corta el eje y en el punto y = f(0), es decir, la parábola corta el eje y cuando x vale cero (0):

$y = f(0) = a \cdot 0^2 + b \cdot 0 + c \,$

lo que resulta:

$y = f(0) = c \,$

la función corta el eje y en el punto (0, c), siendo c el término independiente de la función.

A este punto de la función también se lo conoce con Ordenada al Origen, ya que se da en los términos.

Intersección con el eje x

La función corta al eje x cuando y vale 0, dada la función

$y = ax^2 + bx + c \,$

es decir:

$y = 0 \quad \longmapsto \quad ax^2 + bx + c = 0 \,$

las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el eje x, que se obtienen, como es sabido, por la expresión:

$x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a}$ .

Si la función no corta al eje x, la fórmula anterior no tiene solución (en los reales).